1 Annex I: Transformation of cohort death into deaths by age
2 Bibliography

1 Annex I: Transformation of cohort death into deaths by age

Textbooks in demography are usually silent on the calculation of deaths by age and sex in cohort-component projections. Deaths in a cohort-component framework are associated with the survival of cohorts of people of the same years of birth; they are, in Lexis’s terms, period-cohort events. Because deaths produced by statistical agencies are normally formatted according to a period-age observation plan, the deaths calculated in a cohort component projection need to be transformed from the former to the latter format. The transformation of cohort deaths into deaths by age and sex can be achieved by applying cohort-separation factors obtained from a life table (see, for example UNPD 2015 for a full set of model life tables).

In this annex, several approaches for transforming deaths observed in a period-cohort observation plan into deaths corresponding to a period-age observation plan. The usual way of performing such transformation is by, first, splitting the events into the corresponding lexis triangles using a suitable factor and, second, re-arranging the lexis triangles into the desired observation plan.

1.1 Cohort separation factors

In a cohort-component projection, the only deaths by age that are available are those that occur within an n-year projection interval to those who are aged x at last birthday when entering the projection period, and are x+n when leaving the projection period. These deaths shall be called cohort deaths (also called period-cohort events, occurring in a period-cohort observation plan)¹.

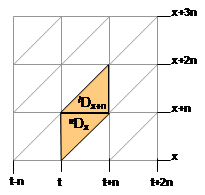
To get deaths by age groups (deaths occurring to those between age x and x+n in the projection period), cohort deaths must be split into their lexis triangles first and then rearranged into the age-period format.

The cohort deaths are composed of two event triangles of the Lexis diagram: The deaths (events) occurring in the upper triangle at age x and the deaths (events) occurring in the lower triangle aged x+n (period-cohort observation plan).

${}_n^c{D_x} = {}_n^u{D_x} + {}_n^l{D_{x + n}}$

Figure 1: Lexis triangles for cohort deaths

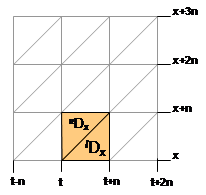
However, we wish to transform the deaths by age obtained from the projection program into the format favored by official statistics, e.g. deaths occurring in the two deaths triangles referring to the same age, or according to the period-age observation plan (E3)

${}_n{d_x} = {}_n^l{D_x} + {}_n^u{D_x}$

Using life table notation, we define lower and upper triangles of deaths as follows:

Lower Lexis triangle deaths:
$\matrix{ {{}^l{D_x}} \hfill & = \hfill & {n*{l_x} - {}_n{L_x}} \hfill \cr {} \hfill & = \hfill & {{}_n{d_x}*(n - {}_n{a_x})} \hfill \cr }$

Upper Lexis triangle deaths
$\matrix{ {{}^u{D_x}} \hfill & = \hfill & {{}_n{L_x} - n*{l_{x + n}}} \hfill \cr {} \hfill & = \hfill & {{}_n{d_x}*{}_n{a_x}} \hfill \cr }$

Figure 2: Lexis triangles for period deaths

Cohort deaths in a period-cohort format are composed of deaths triangles taken from two adjacent age groups. By expressing the upper and lower Lexis triangle with (known) life table variables, we arrive at a convenient formula for the cohort deaths.

$\matrix{ {{}_n^c{D_x}} \hfill & = \hfill & {{}^u{D_x} + {}^l{D_{x + n}}} \hfill \cr {} \hfill & = \hfill & {\left( {{}_n{d_x}*{}_n{a_x}} \right) + {}_n\left( {{d_{x + n}}*(n - {}_n{a_{x + n}})} \right)} \hfill \cr {} \hfill & = \hfill & {\left( {{}_n{L_x} - n*{l_{x + n}}} \right) + \left( {n*{l_{x + n}} - {}_n{L_{x + n}}} \right)} \hfill \cr }$

${}_n^c{D_x} = {}^u{D_x} - {}^l{D_{x + n}} = {}_n{L_x} - {}_n{L_{x + n}}$

Cohort deaths, expressed in terms of life table quantities, are the difference between two adjacent age groups of the life table stationary population (e.g. the person-years lived of the life table).

We now define a separation factor for splitting the cohort deaths into their triangle components. Analogous to the life table separation factor, we define the ratio of lower triangle to total cohort deaths²

$\matrix{ {{}^c{{\rm{f}}_x}} \hfill & = \hfill & {{{{}^u{D_x}} \over {{}^c{D_x}}}} \hfill \cr {} \hfill & = \hfill & {{{{}^u{D_x}} \over {{}^l{D_x} + {}^u{D_{x + n}}}}} \hfill \cr }$

Expressed in terms of life table variables, the cohort separation factor ${}^c{{\rm{f}}_x}$ is

${}^c{{\rm{f}}_x} = {{{}_n{L_x} - n*{l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}{\rm{ }}$ .

Equivalently, the complement $1 - {}^c{{\rm{f}}_x}$ may be expressed as

${\rm{1 - }}{}^c{{\rm{f}}_x} = {{n*{l_{x + n}} - {}_n{L_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}$

The cohort separation factors allow to split the (known) cohort deaths by age into their triangle components:

$\matrix{ {{}^u{D_x}} \hfill & = \hfill & {{}^c{D_x}*{}^c{{\rm{f}}_x}} \hfill \cr {{}^l{D_x}} \hfill & = \hfill & {{}^c{D_{x - n}}*\left( {1 - {}^c{{\rm{f}}_{x - n}}} \right)} \hfill \cr }$

Now we can derive a compact formula for calculating deaths by age from cohort deaths by age

$\matrix{ {{}_n{d_x}} \hfill & = \hfill & {{}^l{D_x} + {}^u{D_x}} \hfill \cr {} \hfill & = \hfill & {{}_n^c{D_{x - n}}*\left( {1 - {}^c{{\rm{f}}_{x - n}}} \right)} \hfill \cr {} \hfill & {} \hfill & { + {}_n^c{D_x}*{}^c{{\rm{f}}_x}} \hfill \cr }$

Replacing the cohort separation factors by their life table quantities, we arrive at:

$\matrix{ {{}_n{d_x}} \hfill & = \hfill & {{D_{x - n}}*\left[ {{{n*{l_x} - {}_n{L_x}} \over {{}_n{L_{x - n}} - {}_n{L_x}}}} \right] + {}_n^c{D_x}*\left[ {{{{}_n{L_x} - n*{l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}} \right]} \hfill \cr }$

And after some rearrangements:

$\matrix{ {{}_n{d_x}} \hfill & = \hfill & {{{{}_n^c{D_{x - n}}*\left( {n*{l_x} - {}_n{L_x}} \right) + {}_n^c{D_x}*{}_n\left( {{L_x} - n*{l_{x + n}}} \right)} \over {{}_n{L_{x - n}} - {}_n{L_x}}}} \hfill \cr }$

Note that, in a cohort-component setting, the deaths by age are the equivalent of the life table deaths _nd_x., e.g. ${}_n{d_x} \buildrel \wedge \over = {}_n{D_x}$

The approach outlined above was first employed in the context of improving the treatment of deaths in the UNPD Abacus in the late 1990s. It is the same as the one presented in the HMD Method Protocol (Wilmoth et al. 2007).

1.2 Cohort separation ratios

A slightly different approach was suggested by K. Andreev (personal communication). It defines the factor to split the events into corresponding Lexis triangles differently, but is, after some transformation, equivalent to the previous approach. It is here called the cohort separation ratio.

Define ${}_n{y_x}$ as the ratio y of lower triangle aged x+n to upper triangle aged x.

$\matrix{ {{}_n{y_x}} \hfill & = \hfill & {{{{}_n^l{D_{x + n}}} \over {{}_n^u{D_x}}}} \hfill & = \hfill & {{{n*{l_{x + n}} - {}_n{L_{x + n}}} \over {{}_n{L_x} - n*{l_{x + n}}}}} \hfill \cr }$

Alternatively, the cohort separation ratio y can be expressed as

$\matrix{ {{}_n{y_x}} \hfill & = \hfill & {{{{}_n{d_{x + n}}*\left( {n - {}_n{a_{x + n}}} \right)} \over {{}_n{d_x}*{}_n{a_x}}}} \hfill \cr }$

Another expression is based on the ${}_n{a_x}$ and ${}_n{q_x}$ :

$\matrix{ {{}_n{y_x}} \hfill & = \hfill & {{{n - {}_n{a_{x + n}}} \over {{}_n{a_x}}}*{{1 - {}_n{q_x}} \over {{}_n{q_x}}}*{}_n{q_{x + n}}} \hfill \cr }$

By using the cohort separation ratio ${}_n{y_x}$ , cohort deaths can now be split into their constituent triangles. The upper triangle is calculated as follows:

$\matrix{ {{}_n^u{D_x}} \hfill & = \hfill & {{{{}_n^c{D_x}} \over {1 + {}_n{y_x}}}} \hfill & = \hfill & {{}_n^c{D_x}*\left( {{1 \over {1 + {}_n{y_x}}}} \right)} \hfill \cr }$

and the lower triangle as:

${}_n^l{D_{x + n}} = {}_n^c{D_x}\left( {{{{}_n{y_x}} \over {1 + {}_n{y_x}}}} \right)$

It will be shown next that the expression $1/\left( {1 + {}_n{y_x}} \right)$ is identical with the cohort separation factor ${}^c{{\rm{f}}_x}$ introduced above.

The expression $1/\left( {1 + {}_n{y_x}} \right)$ for the cohort separation ratio can be written explicitly as

${1 \over {1 + {}_n{y_x}}} = {1 \over {1 + \left( {{{n*{l_{x + n}} - {}_n{L_{x + n}}} \over {{}_n{L_x} - n*{l_{x + n}}}}} \right)}}$

Simplifying and rearranging the expression on the right side we arrive at:

${1 \over {1 + {}_n{y_x}}} = {{{}_n{L_x} - n*{l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}$

Recalling the definition of the cohort separation factor

${\rm{f}}_x^c = {{{}_n{L_x} - n*{l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}$ we see the equivalency between cohort separation factor and cohort separation ratio:

${1 \over {1 + {}_n{y_x}}} = {\rm{f}}_x^c$

1.3 Correspondence between cohort separation factor and fraction of last year of life

It is easy to see that cohort separation factor ( ${}^c{{\rm{f}}_x}$ ) and the fraction of last year of life (_na_x) are similar, but not the same:

${}_n{a_x} = {{{}_n{L_x} - n*{l_{x + n}}} \over {{l_x} - {l_{x + n}}}}$

${}_n^c{{\rm{f}}_x} = {{{}_n{L_x} - n*{l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}$

Both share the same numerator, but differ in their denominator. The denominator of the fraction of last year of life – life table deaths – is equivalent with deaths by age. The denominator of the cohort separation factor is equivalent with cohort deaths in a cohort-component projection framework.

They can be transformed into each other using the following relationships: The fraction of last year of life (_na_x) is obtained by multiplying the cohort separation factor ( ${}_nf_x^c$ ) with the proportion of life table cohort deaths to life table deaths by age. Conversely, the cohort separation factor ( ${}_nf_x^c$ ) can be derived by multiplying the fraction of last year of life (_na_x) with the proportion of the life table deaths by age to life table cohort deaths:

${}_n{a_x} = {}^c{{\rm{f}}_x}*\,\,\left[ {{{{}_n{L_x} - {}_n{L_{x + n}}} \over {{l_x} - {l_{x + n}}}}} \right]$

${}^c{{\rm{f}}_x}\, = {}_n{a_x}*\left[ {{{{l_x} - {l_{x + n}}} \over {{}_n{L_x} - {}_n{L_{x + n}}}}} \right]$

2 Bibliography

Keyfitz, Nathan. 1968. Introduction to the Mathematics of Population. Reading, Mass.: Addison-Wesley.

UNPD (2015). Extended Model Life Tables (Version 1.3). United Nations Population Division, New York. https://esa.un.org/unpd/wpp/Download/Other/MLT/.

Wilmoth, John R, K Andreev, D A Jdanov, and D A Glei. 2007. “Methods Protocol for the Human Mortality Database (Version 5).” Berkeley, CA; Rostock, Germany. http://www.mortality.org/.

Another cohort observation plan is the cohort-age plan, which includes the cohort events happening between exact age x and exact age x+n. This observation plan includes n time periods and is not considered here.↩
This cohort separation factor differs from the one Keyfitz (1968, p. 11) suggested. Keyfitz’s separation factor splits the cohort events observed under a Cohort-Age plan (which span over two periods). It is also different from the one defined in the Human Mortality Database. The latter factor is intended to split Period-Age events into Lexis triangle. In this document, the focus is to split period-cohort events into triangle events occurring during one period.↩